Casino Utan Svensk Licens 2024 – Jämför Bästa Casinon Utan Spelpaus
Välkommen till den ultimata guiden om casino utan svensk licens 2024! Är du en av de tusentals svenska spelarna som letar efter spänningen och friheten som casinon utan Spelpaus erbjuder? Då är den här guiden för dig!
Här kommer vi att avslöja varför allt fler svenska spelare väljer att utforska casinon utan svensk licens spännande spelvärld. Dyk in i en värld av obegränsade spelmöjligheter tillsammans med oss!
Lista med Säkra Casinon Utan Svensk Licens 2024
- All
Bäst Casinon Utan Svensk Licens
Bäst Casinon Utan Svensk Licens
- Spela Utan Spelpaus
- Flera Bonusar och Kampanjer
- Säkra och Smidiga Betalningsmetoder
Bästa Casinon med BankID
Bästa Casinon med BankID
- Spela Utan Registrering
- Stora Spelutbud
- Enorma Casinobonusar
Nya Casinon Utan Svensk Licens
Nya Casinon Utan Svensk Licens
- Fördelaktiga Bonuserbjudanden
- Större Utbud av Casinospel
- Casinon med Direkta Uttag
Bästa Bettingsidor Utan Svensk Licens
Bästa Bettingsidor Utan Svensk Licens
- Betting Utan Svensk Licens och Spelpaus
- Spela på Hundratals Sporter
- Stora Utbud med Bettingbonusar
Bästa Krypto Casinon
Bästa Krypto Casinon
- Helt Anonymt Spelande
- Direkta Insättningar & Uttag
- Enorma Kryptobonusar
Bästa Casinobonusar
Bästa Casinobonusar
- Bonusar Utan Insättning
- Bonusar med Låga Omsättningskrav
- Flera Erbjudanden från Varje Casino
Bästa Casinon med Kreditkort
Bästa Casinon med Kreditkort
- Spela Nu, Betala Senare
- VISA/Mastercard Casinon
- Säkra och Snabba Transaktioner
Bästa Casinon Utan Konto
Bästa Casinon Utan Konto
- Spela Direkt Utan Konto
- Casinon Utan Verifiering
- Enorma Utbud av Casinospel
Bästa Casinon med PayPal
Bästa Casinon med PayPal
- Snabba Insättningar och Uttag
- Säkra Transaktioner
- Välutrustade Bonusutbud
Bästa Pay N Play Casinon
Bästa Pay N Play Casinon
- Sätt in Pengar och Spela Direkt
- Spela Utan Konto
- Stora Välkomstbonusar
Bästa Bettingsidor
Bästa Bettingsidor
- Betting Utan Spelpaus
- Spela på Flera Hundratals Sporter
- Generösa Lojalitetsprogram
Bästa Casinon med Snabba Uttag
Bästa Casinon med Snabba Uttag
- Casinon med Direkta Uttag
- Snabba och Säkra Utbetalningar
- Höga Bonusar med Låga Krav
Bästa Casinon Utan BankID
Bästa Casinon Utan BankID
- Spela Casino Anonymt
- Snabba Insättningar & Uttag
- Stort Utbud av Underhållning
18+. Spela ansvarsfullt. Kontakta Stödlinjen (020-81 91 00) om du eller någon du känner har spelproblem. Vi kan tjäna pengar på att du klickar på länkar utan att det kostar dig något.
5 Rekommenderade Casino Utan Svensk Licens 2024
Att hitta det bästa casinot utan svensk licens kan vara svårt. Våra spelexperter har valt ut de bästa casinon utan svensk licens i 2024 inom olika kategorier, för att göra det enklare för våra läsare. Här är våra topp 5 rekommenderade casinon utan svensk licens.
- Mega Dice – ️️ Casino Utan Spelpaus
- Supacasi – Casino Utan Registrering
- Cashalot – Casino med Snabba Uttag
- Everygame – Betting Utan Svensk Licens
- Overload – Skattefria Casino
Snabbinfo om Casino Utan Svensk Licens
| Säkra Casinon utan Svensk Licens | 165+ |
| Utländska Casinon utan Konto | 120+ |
| Nya Casinon utan Svensk Licens | 15 ( 2024 ) |
| Maximal Casinobonus | €25 000 + Free Spins |
| Max Antal Free Spins | 2 475 + |
| Lojalitetsprogram & VIP-Bonusar | JA |
| Säkra Casinolicenser | MGA, CGA, EMTA, UKGC, m.m |
| Casinospel | Alla |
| Betalningsmetoder | Kort, E-plånböcker, Krypto, Faktura, m.m |
| Genomsnittliga Uttagstid | 30 minuter |
| Skatt på Casinovinster | Utanför EU/EES |
| Casino utan Spelpaus med | GamBlock, GamBan, BetFilter, m.m |
Hur Vi Analyserar Casinon Utan Svensk Licens och Spelpaus
Här avslöjar vi hur våra casinoexperter noggrant granskar och rankar de bästa casinon utan svensk licens och Spelpaus. Vi tar på oss detektivhatten och utforskar varje aspekt av dessa online casinon för att garantera att du får maximalt värde för dina pengar och en säker spelupplevelse. Häng med här så går vi igenom vilka kriterier casinoexperter använder när de rankar casinon utan Spelpaus!
1. Licens och säkerhet
När våra casinoexperter undersöker ett casino utan svensk licens, är det av yttersta vikt att de noga granskar licensieringen och säkerhetsåtgärderna. De tar också hänsyn till vilken jurisdiktion casinot opererar under och bedömer licensmyndigheternas trovärdighet och tillförlitlighet.
Dessutom utför de en grundlig utvärdering av casinots krypteringsprotokoll och dataskyddsåtgärder för att säkerställa det absoluta skyddet av våra läsares personliga och finansiella information.
2. Bonusar och kampanjer
Vi förstår verkligen vikten av attraktiva bonusar och kampanjer för att förbättra den övergripande casinoupplevelsen. Våra experter genomför en noggrann utvärdering av bredden och generositeten hos välkomstbonusar, löpande kampanjer, lojalitetsprogram och VIP-bonusar som erbjuds av varje online casino utan licens i Sverige.
De granskar även villkoren noggrant för dessa erbjudanden för att säkerställa full transparens och rättvisa bonusvillkor. Våra läsare kan vara säkera på att vi levererar den mest insiktsfulla och pålitliga informationen för att hjälpa de att fatta välgrundade beslut när det gäller att spela casino utan Spelpaus.
3. Casinospel och Spelutvecklare
Variationen och kvaliteten på casinospel är avgörande för att bedöma den övergripande kvalitén hos ett casino utan svensk licens. Våra experter genomför omfattande granskningar av spelutbud för att bedöma variationen av spelautomater, bordsspel, live dealerspel och mycket mer. De lägger även stor vikt kring bevisligen rättvisa casinospel och populära spelutvecklare med bra rykten inom branchen.
4. Användarvänlighet och Mobilcasino
Ett sömlöst och användarvänligt gränssnitt förbättrar spelupplevelsen avsevärt. Våra experter bedömer casinon utan svensk licens och deras casinoappar inom navigerbarhet, responsivitet och intuitivitet. De utvärderar också mobilkompatibilitet och funktionalitet, eftersom vi förstår hur viktigt det är att kunna spela när man är på språng.
5. Betalningsmetoder, Avgifter och Uttagstider
För en bra casinoupplevelse är det avgörande med effektiva och problemfria transaktioner. Våra erfarna casinoexperter analyserar noggrant de tillgängliga betalningsmetoderna, inklusive kreditkort, e-plånböcker, kryptovalutor, banköverföringar och mycket mer.
De utvärderar snabbheten och tillförlitligheten hos insättningar och uttag samtidigt som de beaktar eventuella avgifter eller begränsningar. Med vår expertis kan du vara säker på att få en enastående casinoupplevelse.
6. Unika Funktioner
Vi anser att casinon bör erbjuda något unikt för att sticka ut från konkurrensen, så våra experter identifierar och framhäver eventuella särskiljande funktioner som ett casino utan svensk licens erbjuder spelare. Det kan inkludera innovativa casinospel, exklusiva turneringar eller andra spännande funktioner som tillför värde eller intresse för spelarna.
Genom att utvärdera online casinon utan svensk licens baserat på dessa kriterier ser vårt team av casinoproffs till att vi ger våra läsare korrekta, opartiska och pålitliga rekommendationer. Vi strävar efter att vägleda spelare mot de bästa casinon utan svensk licens som erbjuder en trygg, underhållande och givande online casinoupplevelse.
10 Bästa Casinon Utan Svensk Licens 2024
Ta en titt på vår sammanfattade lista över de bästa casinon utan svensk licens i 2024. Denna lista är resultatet av noggrann forskning och analyser, med fokus på säkerhet, casinospel och enastående användarupplevelse. Låt oss vara din guide och hjälpa dig att navigera genom djungeln av online casinon utan spelpaus. Fortsätt läsa för att upptäcka ditt nästa casino utan svensk licens och ta del av en unik spelupplevelse!
- Mega Dice: Bästa casino utan svensk licens med 200% upp till 1 Bitcoin + 50 FS
- SlotAmba: Bäst Slots casino utan licens i Sverige med 300% upp till €1 000
- Supacasi: Säkert casino utan begränsningar med 150% upp till €500
- Cashalot: Bästa nya casino utan svensk licens med 200% upp till €500 + 50 FS
- 21Bets: Bäst casino utan svensk licens med snabba uttag och 180% Upp till €300
- Skycrown: Casino med kortbetalning och faktura med upp till €250 + 225 Free Spins
- Lucky Block: Bitcoin casino utan licens i Sverige med 200% upp till €10 000 + 50 FS
- BetPlays: Casino med flest bevisligen rättvisa spel och 100% upp till €2 000 + 250 FS
- Overload: Bästa casino för Free Spins med låg insättning och 200% Upp till 500 FS
- Reload Casino: Bästa casino utan omsättningskrav med 10% Cashback varje vecka
Casino Utan Svensk Licens i ett Nötskal
Ett casino utan svensk licens är ett casino som inte har erhållit licens från Spelinspektionen. Det innebär att det inte följer de strikta regler och begränsningar som gäller för casinon med svensk licens. Men vad innebär det egentligen?
Casinon utan svensk licens kan erbjuda ett betydligt bredare spelutbud av flera anledningar. Först och främst opererar dessa casinon under licenser utfärdade av seriösa och respekterade tillsynsmyndigheter som Malta Gaming Authority eller UK Gambling Commission. Dessa licenser ger casinon möjlighet att erbjuda ett omfattande utbud av spel från olika leverantörer, inte bara de som är godkända av Spelinspektionen.
Dessutom har casinon utan svensk licens betydligt färre begränsningar när det gäller kampanjer och casinobonusar. Detta innebär att de kan erbjuda ett överflöd av generösa bonusar, attraktiva lojalitetsprogram och lockande VIP-bonusar.
Att spela på ett casino utan svensk licens ger dig också möjligheten att spela utan begränsningar som Spelpaus. Spelpaus, vilket är obligatoriskt för svenska casinon, ger spelare möjlighet att själva stänga av sig från allt spel om pengar och all direktreklam för spel. Däremot är casinon utan svensk licens inte bundna av Spelpaus och kan därför erbjuda en kontinuerlig spelupplevelse, vilket kan vara attraktivt för de som föredrar en mer oavbruten upplevelse.
Det är viktigt att notera att casinon utan svensk licens inte saknar ansvarsfulla spelåtgärder. Tvärtom, de har en annan uppsättning regler att följa som säkerställer en säker och ansvarsfull spelupplevelse. Dessa casinon erbjuder utländska verktyg som GamBan och BetFilter för att aktivt hjälpa spelare att hantera sitt spelande.
Utöver det så kan svenska casinon bara erbjuda ett fåtal betalningsalternativ på grund av lagkrav. Men casinon utan svensk licens kan erbjuda en bredare variation av betalningsmetoder. Dessa inkluderar allt från traditionella metoder som banköverföring och kreditkort till moderna lösningar som e-plånböcker och kryptovalutor. Med dessa alternativ kan du välja den betalningsmetod som passar dig bäst och njuta av en smidigare spelupplevelse.
Så Funkar Casino Utan Svensk Licens i Sverige
Casinon utan svensk licens utgör spelplattformar som inte har erhållit tillstånd från Spelinspektionen. Trots detta kan de erbjuda sina tjänster till svenska spelare. Dessa casinon är vanligtvis licensierade av andra länder, främst inom EU/EES-området, exempelvis Malta, Storbritannien eller Estland.
När det handlar om att spela på dessa casinon, finns det några viktiga saker att ha i åtanke som vi kommer gå igenom nedan:
- Begränsningar och Regler
Casinon utan svensk licens har vissa begränsningar och regler att följa, även om de skiljer sig från dem i Sverige. De måste följa lagstiftningen i det land de är licensierade, vilket kan innebära olika regler om spelgränser, marknadsföring, bonuserbjudanden och ansvarsfullt spelande.
Även om svenska casinon följer noga regler och begränsningar fastställda av Spelinspektionen, kan casinon utan svensk licens njuta av större frihet när det gäller deras kampanjer, betalningslösningar, spelutbud och mycket mer.
Detta innebär att de kan erbjuda generösa bonusar, fler kampanjer och ett bredare spektrum av spelalternativ. Det är värt att notera att de inte är tillåtna att rikta sin marknadsföring till svenska spelare, erbjuda kundsupport på svenska eller ha svenska språket på sin webbplats.
- Självuteslutning
Casinon utan svensk licens är inte kopplade till Spelpaus, den svenska självuteslutningsplattformen. Detta innebär att spelare som har självuteslutit sig genom Spelpaus fortfarande kan spela på casinon utan svensk licens.
Casinon utan svensk licens tar spelansvar på stort allvar och erbjuder självuteslutningsverktyg för att hjälpa spelare att hålla kontroll över sitt spelande. Med internationellt erkända verktyg som GamStop, GamBan, GamBlock, BetFilter och BetBlocker kan spelare känna sig trygga.
- Ingen Skatt på Casinovinster i EU/EES
En stor fördel med casinon utan svensk licens som är licensierade inom EU/EES, är att de erbjuder skattefria vinster. Detta betyder att du inte behöver betala skatt på dina vinster om du spelar på dessa casinon.
Observera att skattereglerna varierar beroende på casinots licens. Inom EU/EES-området är vinster skattefria för svenska spelare. Utanför detta område måste svenska spelare betala 30% skatt på sina vinster.
- Alla Kan Spela på Casino Utan Svensk Licens & Det är Lagligt
Ja, det är faktiskt sant! För svenska spelare är det helt lagligt att spela på casinon utan svensk licens. Som vi har nämnt får casinon utan svensk licens inte marknadsföra sig mot svenska spelare men som spelare har man friheten att spela vart man vill.
Hur Man Skapar Konto på Casino Utan Svensk Licens
Att skapa ett konto på ett casino utan svensk licens är en snabb och enkel process. Det krävs minimalt med personuppgifter och processen är så snabb att utländska casinon ofta klassas som casinon utan konto. Nedan följer en steg-för-steg guide som tar dig genom hela processen från insättning till uttag.
✅ 1. Välj Ditt Bästa Casino Utan Svensk Licens
Första steget i processen är att hitta det casino som passar dig bäst. Olika casinon erbjuder unika upplevelser, spelutbud och bonusar, så det är viktigt att välja ett casino som uppfyller dina individuella behov och preferenser. För att illustrera denna process kommer vi i denna guide att använda det högst rankade casino utan svensk licens enligt våra casinoexperter.
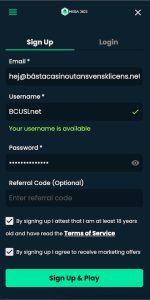
✅ 2. Besök Ditt Online Casino & Skapa Konto
När du har valt ditt casino utan svensk licens, besök deras hemsida. Där finner du vanligtvis en “Sign Up”-knapp på förstasidan. Klicka på den för att påbörja processen med att skapa ditt konto och ta del av alla fördelar.
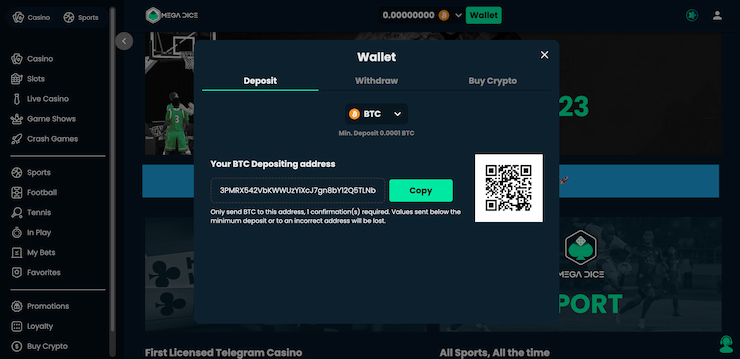
✅ 3. Välj Casinobonus och Gör en Insättning
När du har skapat ditt konto är nästa steg att välja den casinobonus som passar dig bäst. Casinon utan svensk licens erbjuder ofta en rad olika bonusar, från välkomstbonusar till insättningsbonusar och free spins. Välj den bonus som mest tilltalar dig, gör din första insättning för att ta emot bonusen och börja spela utan Spelpaus.
✅ 4. Börja Spela Utan Spelpaus
När du har slutfört insättningsprocessen är det äntligen dags att ta steget in i spelvärlden. På ditt valda casino utan svensk licens kommer du enkelt att navigera genom det breda utbudet av casinospel. Oavsett om du söker efter specifika spel i sökfältet eller utforskar de olika kategorierna, kommer du snabbt att hitta ditt favoritspel.
✅ 5. Ta Ut Eventuella Casinovinster
Att ta ut vinster på ett casino utan svensk licens är en enkel process som liknar insättning. Gå till transaktionssidan och välj “Uttag”. Välj sedan önskad betalningsmetod och fyll i de nödvändiga uppgifterna. Ange det önskade uttagsbeloppet och bekräfta transaktionen. Slutför processen och vänta på att dina vinster överförs till ditt konto.
För-och Nackdelar med Casino utan Svensk Licens
Vi kommer nu att analysera de positiva och negativa aspekterna av att spela på casinon utan svensk licens. Denna sektion ger en jämförande översikt som hjälper dig att ta ett informerat beslut om det är ett online casino utan svensk licens du söker.
Fördelar med Online Casino utan Svensk Licens
- Större Bonusutbud: Casinon utan svensk licens kan erbjuda större och mer generösa bonusar eftersom de inte är begränsade av de strikta regler som gäller för svenska licensierade casinon.
- Ingen Spelpaus: Om du har registrerat dig på Spelpaus men ändå vill spela, kan du göra det på ett casino utan svensk licens.
- Fler Betalningsalternativ: Casinon utan svensk licens har vanligtvis ett bredare utbud av betalningsalternativ.
- Större Spelutbud: Dessa casinon kan erbjuda ett bredare spelutbud eftersom de inte är underlagda de begränsningar som gäller för svenska licensierade casinon.
Nackdelar med Online Casino utan Svensk Licens
- Ingen Tillgång till Spelpaus: Om du har problem med spelberoende kan det vara riskabelt att spela på casinon som inte är kopplade till Spelpaus.
- Olika Spelregler: Eftersom dessa casinon inte följer svenska lagar och regler kan det finnas olika regler och villkor att hålla reda på.
- Ingen Kundtjänst på Svenska: Om du föredrar att interagera med kundtjänst på svenska kan det vara en nackdel att spela på casinon utan svensk licens, eftersom de inte alltid erbjuder svenskspråkig kundservice.
- Skatteregler: Om casinot är licensierat utanför EU/EES-området kan du behöva betala skatt på dina vinster.
Data och Statistik om Casino Utan Svensk Licens och Spelpaus
I detta avsnitt kommer vi att noggrant utforska den senaste statistiken och datan kring casinon utan svensk licens och Spelpaus. Vi kommer att granska olika aspekter, allt från antalet avstängda spelare på Spelpaus till de främsta skälen till varför svenskar väljer att spela på casinon utan Spelpaus.
✅ Antal Avstängda Spelare hos Spelpaus
Den 31 januari 2019 var det inte mindre än cirka 20 000 personer som hade stängt av sig via Spelpaus.se. Men i mars 2023 hade antalet ökat avsevärt till nära 92 000 personer som hade stängt av sig från allt spel om pengar.
Av alla spelare som har valt att stänga av sig från spel med Spelpaus, har hela 71% valt en obestämd avstängningsperiod, 11% valde att vara avstängda i sex månader, medan 10% har valt en avstängning på tre månader. Vi får inte heller glömma de 8% som valde att vara avstängda en månad. Dessa siffror visar på spelarnas starka vilja och medvetenhet, då de aktivt tar ansvar för sitt spelande.
✅ Statistik om Autoplay Funktionen
Nästan hälften (44%) av de deltagare som har spelat på online casinon utan svensk licens har valt att använda autoplay under sitt spelande. Dessutom har över hälften av spelarna enbart använt ett spelkonto för onlinespel på internet de senaste 90 dagarna, medan 30% har rapporterat att de har haft två spelkonton. Detta tydliga mönster pekar på ett växande intresse och visar att allt fler upptäcker fördelarna med nya casino utan svensk licens.
Ungefär en tiondel av deltagarna är medvetna om och har redan använt verktyget Spelpaus, vilket är något fler än vid tidigare mätningar. Hela tre fjärdedelar uppger att de vet vad Spelpaus är, även om de ännu inte har använt det.
✅ Data om Svenska Spelare och Spelproblem
Majoriteten av deltagarna i undersökningen påpekar att de inte har upplevt några problem med sitt spelande under de senaste 12 månaderna. Däremot har spelare som spelar dagligen i högre grad rapporterat att de nästan alltid upplever problem med sitt spelande. Detta tyder på att det är viktigt att vara medveten om de potentiella utmaningar som kan uppstå vid frekvent spelande och vidta lämpliga åtgärder för att hantera detta.
✅ Varför Svenskar Väljer Casino Utan Svensk Licens
Runt 40% av svenska spelare väljer att spela på casinon utan svensk licens för att dra fördel av förmånliga bonuserbjudanden. Detta enligt experter som anser detta vara den viktigaste anledningen. Statistiken visar också en ökning på 7% jämfört med förra året. Andra faktorer att överväga inkluderar:
Cirka 20% av spelarna väljer att spela på casinon utan svensk licens på grund av bättre odds och vinstmöjligheter. Detta är resultatet av de svenska spellagarna, där casinon utan licens i Sverige betalar lägre skatt och därmed har möjlighet att erbjuda bättre odds.
En fjärdedel av alla svenska spelare hos casinon utan svensk licens valde att spela där eftersom de är avstängda hos Spelpaus och inte har några andra alternativ.
En tiondel av spelarna uppger att de kanske inte är säkra på hur man kan avgöra om ett casino har svensk licens. För att bekräfta om ett casino har svensk licens eller inte, rekommenderar vi att du besöker Spelinspektionens webbplats och använder sökfunktionen för att hitta casinot. Detta ger dig en pålitlig och korrekt källa för att verifiera casino-licensen.
Historian Om Casino Utan Svensk Licens
Casinon utan svensk licens är online casinon som inte har en licens från Spelinspektionen. Dessa casinon på nätet regleras istället av andra licensieringsmyndigheter, såsom Malta Gaming Authority eller UK Gambling Commission. Det är viktigt att notera att trots att de saknar svensk licens, är de fortfarande lagliga och säkra att spela på, under förutsättningen att de har en giltig licens från en ansedd myndighet.
En anledning till att vissa spelare föredrar att spela på casinon utan svensk licens är att dessa casinon erbjuder betydligt mer generösa bonusar och kampanjerbjudanden. Det är på grund av att de inte är begränsade av de stränga reglerna som gäller för svenska licensierade casinon sedan det infördes nya spellagar under 2019.
✅ Den Svenska Spelmarknaden Granskas
“En omreglerad spelmarknad” är en rapport från den svenska regeringen som föreslår omfattande reformer av spelbranschens reglering. Rapporten tackar Lotteriinspektionen för deras arbete med förordningar som en del av regeringens uppdrag.
Undersökningen syftar till att öppna upp den svenska spelmarknaden för utländska casinon utan svensk licens genom stora förändringar i lagstiftningen. Det skulle ge utländska casinon möjlighet att ansöka om en casinolicens i Sverige.
En annan väsentlig del av rapporten behandlar hastighet och effektivitet i processen för att erhålla licenser för online betting och spelverksamhet. Med den nya regleringen skulle företag, förutom ATG och Svenska Spel AB, kunna ansöka om licenser. Denna reglering öppnar upp för fler företag att delta i denna lukrativa bransch och dra nytta av de möjligheter som erbjuds.
Undersökningen “En omreglerad spelmarknad” föreslår en omfattande reform av den svenska spelmarknaden. Detta förslag innebär betydande lagstiftningsändringar och öppnar upp marknaden för utländska företag, vilket i sin tur främjar ansvarsfullt spelande genom införandet av verktyg och resurser. Genom att implementera dessa åtgärder kommer spelmarknaden att stärkas och skapa en mer dynamisk och konkurrenskraftig miljö.
✅ Blockering av Betalningslösningarna Zimpler, Trustly, Swish och BankID
Svenska spelmarknaden genomgick betydande förändringar under 2024, med en märkbar popularitet av pay n play casino utan svensk licens bland svenska spelare. Regeringen vidtog beslutsamma åtgärder för att bekämpa olaglig spelverksamhet och spelberoende, vilket tydligt visar engagemang för en sund och säker spelmarknad.
Lagändringar har framgångsrikt genomförts för att säkerställa en trygg spelmarknad för svenska konsumenter och effektivt reglera den, med särskilt fokus på betaltjänstleverantörer som Trustly och Zimpler. Spelinspektionen har nu befogenhet att blockera dessa och andra betaltjänster från casinon utan svensk licens.
✅ De Nya Svenska Spellagarna Träder i Kraft
År 2019 innebar en betydande omreglering av spelmarknaden i Sverige genom införandet av ett licenssystem. Den 1 januari trädde en ny spellag i kraft som krävde att alla företag som ville erbjuda spel till svenska spelare måste inneha en licens från Spelinspektionen. Syftet med detta var inte bara att stärka regleringen av spelindustrin, utan också för att förse spelare med en tryggare och mer pålitlig spelupplevelse.
Införandet av Spelpaus.se var ett betydelsefullt steg för att ge spelare möjlighet att själva utesluta sig från licensierat spel. Denna framstående tjänst introducerades som en central del av de nya reglerna i början av 2019.
År 2019 innebar betydande förändringar inom den svenska spelindustrin med fokus på att skapa en mer hållbar och ansvarsfull spelmarknad. Dessa händelser har spelat en avgörande roll och satt igång en i överlag positiv utveckling i rullning.
Casino Utan Spelpaus i ett Nötskal
Casino utan Spelpaus är online casinon som, då de inte har licens från Spelinspektionen i Sverige, inte är anslutna till Spelpaus-systemet. Detta innebär att de kan erbjuda spelare en alternativ möjlighet att spela utan Spelpaus.
Spelpaus är en nationell självuteslutningstjänst som hjälper svenska spelare att ta en paus från allt spelande med pengar. Men genom att välja ett casino utan Spelpaus har spelare möjligheten att utforska andra spelupplevelser och alternativ.
Men vet du vad som händer om du vill fortsätta spela trots Spelpaus? Det är här casinon utan svensk licens kommer in i bilden. Då de inte är licensierade av Spelinspektionen, är de inte bundna av Spelpaus-reglerna. Det betyder att spelare som har självuteslutit sig genom Spelpaus fortfarande kan spela på dessa online casinon.
Även om dessa casinon strävar efter att erbjuda en underhållande och spännande spelupplevelse, är de också medvetna om vikten av ansvarsfullt spelande. Genom att erbjuda sina egna verktyg för självuteslutning och spelgränser hjälper de spelare att hålla sitt spelande under kontroll. Detta visar deras engagemang för spelarsäkerhet och ansvarsfullt spelande.
Hur Spelpaus Funkar
Spelpaus ger individer möjligheten att själva utesluta sig från alla licensierade spel om pengar i Sverige. Det omfattar både online casinon och fysiska spelplatser. Under den valda tidsperioden blir det omöjligt för dem att logga in eller skapa nya konton på svenska casinon eller appar.
Direktmarknadsföringsmaterial som är kopplat till spel kommer också att blockeras. En avstängning med Spelpaus kan inte avslutas. Det är en kraftfull åtgärd som ger dig kontroll över ditt spelande och visar ditt engagemang för ett ansvarsfullt och säkert spelande.
Personuppgifter
Vid registrering på Spelpaus krävs att du anger personuppgifter såsom ditt personnummer och e-postadress. Dessa uppgifter används för att säkerställa en effektiv uteslutning från spelplattformar samt förhindra direktmarknadsföring relaterad till spel. Notera att Spelinspektionen iakttar GDPR vid behandling av dina personuppgifter för att skydda din integritet.
Tekniskfunktion
Spelpaus fungerar genom att skapa en säker databas där individer som valt att utesluta sig från spel kan registreras. När någon försöker logga in eller skapa ett konto på en spelplattform, kontrolleras deras uppgifter mot databasen. Om det finns en matchning blockeras deras åtkomst till spelplattformen.
Spelpaus erbjuder ett tillförlitligt och effektivt system som ger individer möjlighet att avstå från spel med trygghet och skydd som många andra utländska alternativ till Spelpaus.
Guide Till att Stänga av Sig Från Spel med Spelpaus
Följ denna enkla guide för att säkerställa en problemfri process när du vill stänga av dig från spel om pengar med Spelpaus.
1. Besök Spelpaus
För att inleda processen, besök Spelpaus.se. Detta är den officiella webbplatsen för självuteslutningstjänsten, tillhandahållen av Spelinspektionen.
2. Välj En Tidsperiod
Här kommer du att få möjlighet att välja hur länge du vill ha din spelavstängning. Du kan välja mellan 1, 3, 6 månader, eller tills vidare.
3. Bekräfta Din Identitet
För att garantera säkerhet och effektiv självuteslutning, kommer du att bli ombedd att bekräfta din identitet. Detta kan vanligtvis göras genom att använda BankID.
4. Godkänn Avstängningsperioden
Efter att du har bekräftat din identitet, är det dags att godkänna avstängningsperioden. När du har gjort detta, börjar avstängningsperioden omedelbart och du kommer inte ha tillgång till licensierade spelplatser under den valda perioden.
Med dessa enkla steg kan du ta kontroll över ditt spelande och säkerställa ett mer ansvarsfullt spelsätt.
Man kan INTE Avsluta en Påbörjad Avstängning med Spelpaus
När du tar beslutet att registrera dig för en spelavstängning med Spelpaus, är det viktigt att du har full förståelse för att denna åtgärd inte kan ångras. Det är en kraftfull mekanism som är utformad för att erbjuda ett starkt skydd för spelare och främja ansvarsfullt spelande. När du väl har påbörjat din avstängningsperiod finns det ingen möjlighet att återvända till spelandet förrän perioden har löpt ut. Med Spelpaus kan du vara trygg i vetskapen om att du tar ansvarsfulla beslut för ditt eget välbefinnande.
Det innebär att oavsett omständigheterna kan du inte avsluta din avstängningsperiod i förtid. Detta skyddar dig från att potentiellt agera impulsivt eller frestas att återvända till spelandet för tidigt. Detta är ett viktigt steg för att säkerställa att du tar full kontroll över ditt spelande och ger dig tid att reflektera över dina spelvanor på ett mer effektivt sätt.
Kom ihåg att avstängningen gäller även direktmarknadsföringsmaterial kopplat till spel, vilket effektivt minimerar frestelser att spela under denna period. Att fullt ut förstå och acceptera betydelsen av denna avstängning är en central del av att ta ansvar för ditt spelande och säkerställa att du spelar på ett säkert och ansvarsfullt sätt.
Antal Casinon Utan Spelpaus
Även om det finns regler kring Spelpaus, är det fortfarande ett väldigt stort antal av casinon utan Spelpaus. Det är viktigt att förstå att dessa casinon inte omfattas av svensk lagstiftning och kan innebära vissa risker.
Bästa Casinon Utan Spelpaus 2024
Våra casinoexperter har granskat och bedömt flera av dessa casinon och vi kan därför ge några rekommendationer. De bästa casinon utan Spelpaus enligt våra experter är Mega Dice, SlotAmba och SupaCasi. Dessa erbjuder en bred variation av spel, har en stark kundtjänst och erbjuder många olika betalningsmetoder.
Kom ihåg att det alltid är avgörande att spela ansvarsfullt, oavsett om du spelar på ett casino med svensk licens eller på ett casino utan svensk licens. Det är viktigt att vara medveten om dina val och göra informerade beslut när du spelar.
Alternativ Till Spelpaus hos Casinon Utan Spelpaus
Även om Spelpaus är en effektiv metod för att begränsa spelandet, finns det naturligtvis de som föredrar alternativ, särskilt på casinon utan svensk licens. Lyckligtvis finns det flera internationella alternativ tillgängliga som liknar Spelpaus. Här är några av de mest populära alternativen:
GamStop
GamStop är en framstående och kostnadsfri tjänst baserad i Storbritannien. Den ger spelare möjlighet att själva utesluta sig från alla online casinon som är licensierade av UKGC (United Kingdom Gambling Commission).
Med GamStop kan du ta kontroll över ditt spelande genom att inte kunna logga in på ditt befintliga konto eller skapa ett nytt konto på någon av dessa webbplatser. Det är ett kraftfullt verktyg för att skydda dig själv och ta ansvar för ditt spelande.
GamBan
GamBan erbjuder programvara som effektivt blockerar åtkomsten till alla online casino. Det är det perfekta valet för de som vill ta en välbehövlig paus från spelandet. Trots att det inte är gratis, erbjuder det en otroligt förmånlig kostnad i förhållande till den exceptionellt höga skyddsnivån det ger.
GamBlock
GamBlock har en något annorlunda strategi. Det är en programvara som du kan installera på din dator eller mobila enhet för att automatiskt blockera åtkomst till casinon på nätet. Även om det inte är gratis, har det funnits i många år och har fått gott om positiva recensioner.
BetBlocker
BetBlocker är ett fantastiskt användbart och kostnadsfritt verktyg som effektivt blockerar tusentals online casinon. Dessutom erbjuder det stöd för flera plattformar och ger användarna möjlighet att välja en individuellt anpassad uteslutningsperiod som passar deras behov. Med BetBlocker kan du känna dig trygg och säker i din strävan efter att kontrollera ditt spelande.
BetFilter
BetFilter är en speciellt designad lösning som effektivt blockerar åtkomst till online casinon och filtrerar bort allt spelrelaterat innehåll. Detta premiumprogram erbjuder en reklamfri upplevelse och enligt deras webbplats, inga falska positiva. Med BetFilter kan du tryggt och säkert skydda dig från frestelsen av online-spel.
Alla dessa verktyg är effektiva på sitt eget sätt och erbjuder ett starkt skydd för de som vill kontrollera sitt spelande. Det är viktigt att notera att de flesta av dessa verktyg kräver en viss nivå av teknisk kunskap att installera och använda effektivt. Om du har några svårigheter kan du alltid kontakta verktygets kundtjänst för hjälp.
Hur Man Stänger av Sig Från Spel på Casino Utan Spelpaus
Om du behöver ta en paus från spelandet och spelar på casinon som inte omfattas av Spelpaus, finns det alternativ tillgängliga för dig. Du kan inte bara begränsa ditt spelande på casinon med svensk licens, utan även på de utan svensk licens. I följande avsnitt kommer vi att utforska de två huvudsakliga metoderna för att göra detta: att begära avstängning via kundsupport och att använda internationella alternativ till Spelpaus.
Hur Man Stänger av Sig Från Spel Via Kundsupport På Casinon Utan Svensk Licens
För att ta en paus från spelandet eller att helt stänga av sig från ett casino utan svensk licens via deras kundsupport, följ dessa steg:
- Kontakta Kundtjänsten: Vanligtvis finns det flera sätt att nå kundtjänst – via live-chatt, e-post eller telefon. Du kan hitta deras kontaktinformation på casinots webbplats.
- Förklara Situationen: När du kontaktat kundtjänst, förklara att du vill pausa ditt konto eller stänga av dig permanent från casinot. Var tydlig med dina skäl för att undvika missförstånd.
- Bekräfta Din Identitet: Casinot kommer förmodligen att be dig att bekräfta din identitet. Detta är för att säkerställa att det verkligen är du som begär denna åtgärd.
- Följ Deras Instruktioner: Kundtjänsten kommer att ge dig instruktioner om hur du går vidare. Följ dessa noggrant.
- Bekräftelse: När processen är klar, bör du motta en bekräftelse från casinot att du har blivit avstängd.
Självuteslutning Från Spel på Casinon Utan Spelpaus med andra Alternativ
Om du vill ta full kontroll över ditt spelande och aktivt stänga av dig från online casinon som inte följer svensk lagstiftning, finns det ett antal internationella självuteslutningstjänster som du kan använda. Här är några grundläggande steg för att registrera dig för dessa tjänster och ta makten över din spelupplevelse.
GamStop, GamBan, GamBlock, BetBlocker, BetFilter:
- Besök Verktyget: Gå till tjänstens officiella webbplats.
- Registrera Dig: Klicka på “Registrera” eller “Sign Up” och fyll i nödvändig information.
- Välj Uteslutningsperiod: Beroende på tjänsten, kommer du att erbjudas att välja en uteslutningsperiod. Välj den period som passar bäst för dina behov.
- Bekräfta Din Registrering: Du kommer förmodligen att få en e-post med en bekräftelse. Klicka på länken i e-posten för att slutföra processen.
- Installera Programvaran (om tillämpligt): Om tjänsten är en programvara som GamBan, GamBlock eller BetFilter, kommer du att behöva ladda ner och installera den på dina enheter.
Tänk på att dessa tjänster inte utgör en definitiv lösning för problematiskt spelande. Om du brottas med spelproblem, var inte rädd att söka professionell hjälp. Det finns experter som är skickliga inom området och kan ge dig den vägledning och stöd du behöver.
Symptom vid Spelberoende
Spelberoende är en allvarlig psykisk ohälsa som kan få långtgående konsekvenser för en individs liv. Det är av yttersta vikt att vara medveten om symptomen för att kunna upptäcka problemet i ett tidigt skede och söka hjälp. De vanligaste symptomen inkluderar en okontrollerbar lust att spela, ökad tid ägnad åt spelande, att satsa större summor för att uppnå samma “kick”, svårigheter att minska eller sluta spela samt förlust av intresse för andra aktiviteter.
Ansvarsfullt spelande innebär att ha en välavvägd och rationell inställning till spelandet, och att undvika att det påverkar andra delar av ditt liv negativt. Framför allt bör du aldrig betrakta spel som en pålitlig inkomstkälla. Det är viktigt att förstå och acceptera att spel är en form av underhållning snarare än ett sätt att tjäna pengar. Att ha denna insikt är en central del av ansvarsfullt spelande.
Om du eller någon du känner upplever symptom på spelberoende, tveka inte att söka hjälp. I Sverige finns det en rad olika hjälpverktyg och resurser tillgängliga för de som kämpar med spelberoende. Du är inte ensam och det finns stöd att få.
Stödlinjen
Stödlinjen är en nationell stödtjänst där du kan få professionell hjälp och rådgivning. Vi erbjuder anonym och kostnadsfri rådgivning via telefon, chatt och e-post. Dessutom kan vi förmedla kontakt till behandlingshem och självhjälpsgrupper inom spelberoende. Räkna med att vi har den kunskap och erfarenhet som krävs för att hjälpa dig på bästa möjliga sätt. Vi finns här för att stötta dig genom hela processen och ge dig verktygen du behöver för att ta kontroll över ditt spelberoende.
Stödgrupper
Stödgrupper kan erbjuda kraftfullt stöd genom att koppla samman dig med andra som upplever samma utmaningar. I dessa grupper har du möjlighet att dela dina erfarenheter, lära av andra och känna att du inte är ensam i din kamp. Genom att delta i dessa grupper kan du skapa en starkare känsla av samhörighet och få värdefull insikt för att hantera dina utmaningar på ett framgångsrikt sätt.
Vårdguiden
Vårdguiden, även känt som 1177, erbjuder omfattande information om sjukdomar, professionella råd om hälso- och sjukvård samt praktiska e-tjänster för att boka vårdkontakter. På Vårdguidens webbplats finns en dedikerad sektion om spelberoende, som ger detaljerad information om symptom, utför tester, presenterar olika behandlingsalternativ och ger råd om vart man kan vända sig för att få hjälp. Vi är här för att tillhandahålla den kunskap och stöd du behöver för att hantera spelberoende på ett effektivt sätt.
Kom ihåg att när det kommer till spelberoende är det aldrig för tidigt eller för sent att söka hjälp. Det är ett steg i rätt riktning att ta initiativ och söka stöd för att påbörja din väg mot tillfrisknande. Du är inte ensam, och det finns människor och resurser tillgängliga för att stötta dig på denna resa. Ta det första steget idag och låt oss hjälpa dig på vägen mot ett hälsosammare och lyckligare liv.
Varför Utländska Casinon Inte Söker Svensk Spellicens
Utländska casinon och nordiska casinon utan svensk licens väljer att avstå från att ansöka om licens av flera skäl. En av de främsta anledningarna är den stränga regleringen kring bonusar i Sverige, som begränsar casinos förmåga att attrahera och behålla spelare.
Dessutom är casinon utan licens inte bundna till Spelpaus-systemet, vilket ger spelarna mer frihet. Ansvarsfullt spelande bör dock alltid prioriteras. I följande del av artikeln kommer vi gå igenom de mest vanligt förekommande anledningarna till varför casinon utan svensk licens inte söker en svensk spellicens.
Vanliga Anledningar Varför Utländska Online Casinon inte Söker Svensk Spellicens
Med ett ökande antal casinon som väljer att inte ansöka om svensk spellicens, är det viktigt att veta vad man bör leta efter. Det finns flera anledningar till varför casinon undviker att ansöka om licens i Sverige, och här förklarar vi de vanligaste orsakerna.
Kostnad, Skatt och Avgifter
Kostnaden för att ansöka om svensk spellicens är betydande, uppgående till 400 000 kr. Dessutom är spelskatten i Sverige hög, med en nivå på cirka 32%. Casinon med svensk licens tvingas också betala årliga tillsynsavgifter på över 30 000 kr.
Strikta Regler och Riktlinjer
Ytterligare skäl är de strikta regleringarna och riktlinjerna som casinon med svensk licens måste följa. De kan inte konkurrera med casinon utan svensk licens när det kommer till bonuserbjudanden, då de bara kan erbjuda en bonus per spelare. Dessutom måste svenska casinon tillämpa tresekundersregeln på alla spelautomater och tvinga spelare att sätta insättningsgränser.
Spelinspektionens “Spontana Lagändringar”
Det är också viktigt att notera att Spelinspektionen har befogenhet att ändra och uppdatera reglerna och villkoren vid behov, vilket vi såg under COVID-19-pandemin. Dessutom kan casinon med svensk licens inte erbjuda samma betalningsmetoder för insättningar och uttag som casinon utan svensk licens.
Spelpaus
Slutligen, alla casinon med svensk licens måste vara anslutna till Spelpaus, vilket bidrar till att främja ansvarsfullt spelande.
Casinobonusar Utan Svensk Licens
Casinobonusar utgör en kraftfull strategi som casinon använder för att attrahera nya spelare och belöna sina lojala kunder. Casinon utan svensk licens kan erbjuda ett betydligt mer attraktivt utbud av bonusar jämfört med casinon som är licensierade i Sverige. Detta beror på de restriktioner som Spelinspektionen har infört.
Bonusarna hos casinon utan svensk licens inkluderar välkomstbonusar, insättningsbonusar, gratissnurr, cashbacks, lojalitetsprogram och mycket mer. I den här sektionen kommer vi att analysera alla typer av bonusar på casinon utan svensk licens.
Välkomstbonusar
Välkomstbonusar är kanske den mest kända typen av bonus bland online casinon. De erbjuds till nya spelare och kan bestå av en insättningsbonus, gratissnurr eller en kombination av båda. Dessa bonusar är utformade för att locka nya spelare till casinot.
Insättningsbonusar
Insättningsbonusar erbjuds när en spelare gör en insättning på ett online casino. Casinot matchar spelarens insättning med en viss procentandel, upp till ett maxbelopp. Dessa bonusar kan ge spelare mer att spela för, öka deras chanser att vinna.
Matchningsbonusar
Matchningsbonusar, även kända som insättningsbonusar, är en av de mest förekommande bonusarna på online casinon utan svensk licens. De innebär att casinot matchar spelarens insättning med en viss procent, vanligtvis 100%, men vissa bolag kan erbjuda upp till eller över 300 bonus casino. Dessa bonusar ger spelare extra pengar att spela för, vilket kan öka deras chanser att vinna.
Free Spins
Gratissnurr, eller free spins, är bonusar som ger spelare möjlighet att spela ett visst antal omgångar på utvalda spelautomater gratis. De är populära hos spelare eftersom de ger dem chansen att prova på nya spel utan risk.
Cashbacks
Cashback-bonusar innebär att casinot ger tillbaka en viss procent av spelarens förluster under en bestämd period. De är en populär bonusform bland regelbundna spelare eftersom de kan bidra till att minska förlusterna.
Lojalitetsprogram
Lojalitetsprogram belönar regelbundna spelare för sitt fortsatta spel på casinot. Fördelarna kan omfatta allt från gratissnurr och bonuspengar till inbjudningar till VIP-event och snabbare uttag. Hos casinon utan svensk licens är det inte ovanligt för VIP bonusar och lojalitetsprogram att inkludera biljetter till stora sportevent.
No Deposit Bonus
No Deposit Bonus, eller bonus utan insättning, är en bonus som casinon utan svensk licens ofta utnyttjar för att locka nya spelare. Dessa bonusar tillåter spelare att spela och vinna riktiga pengar utan att behöva göra en insättning. Det är viktigt att notera att dessa bonusar ofta kommer med höga omsättningskrav och vinstbegränsningar.
Rakeback
Rakeback är en annan populär bonus hos casino utan svensk licens. Detta är särskilt vanligt inom online poker och betting utan svensk licens, där casinot returnerar en viss procentandel av den rake eller turneringsavgift som spelaren har satsat. Rakeback kan vara mycket värdefullt för frekventa spelare och bidrar till att förbättra den totala avkastningen.
Oddsboost
Oddsboost är en bonus som huvudsakligen används av bettingsidor utan svensk licens, för att öka värdet av specifika spel. Det innebär att oddsen för vissa händelser ökar, vilket ger spelaren potential att vinna mer pengar än vanligt. Dessa bonusar är ofta tidsbegränsade och gäller för specifika matcher eller händelser.
Skatt på Casinon utan Svensk Licens och Spelpaus
Dyk ner i vårt kommande avsnitt där vi detaljerat tar upp allt du behöver veta om skatt på casinon utan svensk licens och Spelpaus. Upptäck också hur du kan njuta av dina vinster skattefritt på casinon utan svensk licens.
Casinon som är Skattefria Casinon Utan Svensk Licens
Skattefria online casinon utan svensk licens utgörs huvudsakligen av de som är etablerade inom Europeiska Ekonomiska Samarbetsområdet (EES). Dessa inkluderar länder som Malta, Gibraltar och Cypern. Dessa länder har strikta regler och riktlinjer som liknar Sveriges, vilket gör dem till pålitliga online casinon.
Det är viktigt att notera att svenska spelare kan ta del av av skattefria vinster från dessa skattefria casinon i enlighet med EU:s princip om fri rörlighet för varor och tjänster. Det är ett känt faktum att dessa casinon ger spelare trygghet och förtroende, vilket gör dem till ett klokt val för svenska spelare som söker en skattefri spelupplevelse.
Casinon som INTE är Skattefria Casinon Utan Svensk Licens
Casinon som inte är skattefria är de som drivs utanför EES, till exempel från Costa Rica, Curacao eller Kanada. Trots att dessa casinon kan erbjuda frestande bonuserbjudanden och ett brett utbud av spel, är eventuella vinster skattepliktiga i Sverige. Det beror på att dessa länder inte omfattas av EU:s regler om fri rörlighet. Det är därför av största vikt att alltid kontrollera licensen innan man börjar spela på ett casino utan svensk licens.
Hur Spelskatten Fungerar i Sverige
I Sverige beskattas vinster från spel på online casinon utanför EU. Därför är det av yttersta vikt att du kontrollerar casinots licens innan du börjar spela. Om du vinner på ett casino på nätet utanför EU måste du betala 30% av vinsten i skatt. Men om casinot har en licens inom EU, är vinsten skattefri tack vare EU:s princip om fri rörlighet för varor och tjänster.
Detta gäller oavsett vinstens storlek. Därför kan det vara fördelaktigt att välja ett casino utan svensk licens men med licens inom EU om du vill undvika skatt på dina vinster. Skattefria casinon ökar, av ganska uppenbara skäl, i popularitet årligen bland svenska spelare.
Exempel på Casinovinster och Beskattning
För att förklara hur beskattning av casinovinster fungerar i Sverige, låt oss titta på tre olika scenarier.
Vinster på ett Casino på Nätet Utan Svensk Licens inom EES
Föreställ dig att du spelar på ett casino utan svensk licens, men casinot har en licens från Malta, ett EU-land. Om du har turen att vinna 10 000 kr behöver du faktiskt inte betala någon skatt på vinsten, tack vare casinots EU-licens. Det betyder att hela vinstsumman på 10 000 kr blir din att behålla.
Vinster på ett Online Casino Utan Svensk Licens Utanför EES
Föreställ dig att du spelar på ett casino utanför EES som innehar en licens från Curacao. Om du skulle vinna 10 000 kr kommer dina vinster att bli skattepliktiga i Sverige eftersom casinot saknar en EU-licens.
Det innebär att du kommer behöva betala 30% i skatt på din vinst, vilket motsvarar 3 000 kr. Du kommer då endast få behålla 7 000 kr av din vinst. Det är viktigt att vara medveten om dessa skattekonsekvenser när du spelar på ett casino utanför EU.
Vinster på ett Online Casino med Svensk Licens
I det tredje scenariot kan vi förutsätta att du spelar på ett svenskt casino med svensk licens och vinner 10 000 kr. I detta fall behöver du inte betala någon skatt på din vinst, oavsett licensstatus för casinot, eftersom det är ett svenskt casino. Du kan glädjas åt att du kan behålla hela vinstsumman på 10 000 kr.
Dessa exempel belyser vikten av att ha en djup förståelse för spellicensen hos det online casino där du väljer att spela. Genom att medvetet välja kan du optimera dina vinster och undvika onödig beskattning på ett skickligt sätt.
Betalningsmetoder på Casinon Utan Spelpaus
För att erbjuda spelare en smidig och bekväm spelupplevelse presenterar casinon utan Spelpaus ett brett utbud av pålitliga och effektiva betalningsmetoder. Dessa inkluderar allt från traditionella kredit- och betalkort till e-plånböcker, banköverföringar och kryptovalutor.
Varje betalningsmetod har sina egna unika fördelar och nackdelar när det kommer till transaktionsavgifter, transaktionstider och tillgänglighet. Vi strävar efter att tillhandahålla de bästa alternativen för att möta spelarnas behov och önskemål.
Kredit- och Betalkort
Visa och Mastercard är bland de mest populära betalningsmetoderna på casinon utan svensk licens. Dessa kreditkort och betalkort är välkända för sin bekvämlighet och snabba transaktionstider.
Det kan förekomma vissa avgifter beroende på ditt kortutgivande företag och casinot, så det är alltid bäst att kontrollera detta i förväg. Du kan tryggt förlita dig på dessa pålitliga och väletablerade betalningsalternativ för en smidig spelupplevelse.
E-plånböcker
E-plånböcker som Skrill, Neteller och PayPal blir alltmer populära på online casinon tack vare deras snabba casino uttag och höga säkerhet. Transaktionerna är vanligtvis omedelbara och avgifterna är låga eller obefintliga. Det är viktigt att notera att vissa casinon kan ha restriktioner när det gäller att använda dessa metoder för bonusar. Med dessa pålitliga och bekväma e-plånböcker kan du njuta av en smidig och säker spelupplevelse på online casinon.
Banköverföringar
Banköverföringar är en trygg och pålitlig metod som, jämfört med andra alternativ, kan ta något längre tid – vanligtvis mellan 3-5 arbetsdagar. Avgifter kan variera beroende på din bank och det specifika casinot. Det är däremot en väldigt pålitlig och säker transaktionsmetod.
Kryptovalutor
Kryptovalutor som Bitcoin och Ethereum blir allt vanligare accepterade på casinon utan svensk licens. Dessa betalningsmetoder erbjuder både anonymitet och snabba transaktioner och har potential till prisvolatilitet.
Faktura
Att betala via faktura har blivit en oerhört populär metod för svenska spelare att finansiera sitt spelande på casinon utan svensk licens. En betydande fördel med denna metod är att spelarna kan komma igång direkt och sedan betala fakturan inom en given tidsram, vanligtvis 14 dagar.
Det är av yttersta vikt att vara fullt medveten om att det föreligger vissa risker med försenade betalningar, det kan resultera i höga avgifter och räntekostnader om betalningen inte hanteras på korrekt sätt.
SMS Betalningar
SMS-betalningar har blivit alltmer populära på casinon utan spelpaus då de erbjuder en snabb och smidig metod för att sätta in pengar på spelkontot. Genom att skicka ett SMS från din mobil kan du enkelt överföra pengar till ditt casinokonto. Detta tillvägagångssätt är särskilt praktiskt för spelare som föredrar att spela på mobilcasino och ger dig möjligheten att snabbt och enkelt njuta av dina favoritspel när som helst och var som helst.
Förbetalda Kort
Paysafecard är ett utmärkt exempel på ett förbetalt kort som smidigt kan användas på casinon utan svensk licens. Genom att enkelt ladda kortet med önskat belopp kan du snabbt och säkert sätta in pengar på ditt casinokonto. En av de stora fördelarna med denna metod är att den ger dig full kontroll och begränsning av ditt spelande, då du endast kan använda det belopp som finns tillgängligt på kortet.
Det är alltid viktigt att kontrollera tillgängliga betalningsmetoder på det casino utan Spelpaus där man har tänkt spela, man bör åtminstone kontrollera att en betalningsmetod är stödd som man kan göra en insättning med. Läs också noggrant igenom deras villkor för insättningar och uttag för att säkerställa en smidig och bekymmersfri spelupplevelse.
Information som Delas med Skatteverket av Casinon Utan Svensk Licens
I vanliga fall delar casinon utan svensk licens inte aktivt information med Skatteverket. Dessa casinon är oftast verksamma utomlands och omfattas därför inte av Skatteverkets jurisdiktion. Det bör dock påpekas att de ändå inte är helt befriade från svenska lagar och regler.
Om Skatteverket har starka misstankar och laglig grund om skattefusk och begär specifika uppgifter om en spelare från casinot, kan de potentiellt få tillgång till sådan information. Det är dock viktigt att förstå att detta är en ovanlig situation och att det krävs tydliga och lagliga grunder för sådana förfrågningar.
Av den anledningen är det alltid bäst att spela ansvarsfullt och följa skattelagarna för att undvika eventuella problem. Genom att följa lagstiftningen visar du din kunskap och kompetens som spelare och bidrar till att upprätthålla en sund och reglerad spelmarknad.
Användning av SEK på Casinon Utan Spelpaus
Observera att SEK generellt inte accepteras på casinon utan Spelpaus. Dessa casinon är vanligtvis baserade utomlands och tar inte emot svenska kronor som betalningsvaluta. Det kan vara klokt att överväga alternativa betalningsmetoder som euro, dollar eller kryptovalutor för en smidig spelupplevelse. För att undvika eventuella betalningsproblem, är det alltid bäst att dubbelkolla vilka valutor som accepteras innan du registrerar dig.
Blockerade Betalningsmetoder hos Casinon Utan Svensk Licens
En betydelsefull åtgärd som påverkar svenska spelare är nyligen införandet av blockering av vissa betalningsmetoder för casinon utan svensk licens. Spelinspektionen har fått ett förslag godkänt och det trädde i kraft i juni 2023. Det innebär att betalningslösningar som Trustly, Swish, Zimpler och BankID nu är blockerade på casinon utan svensk licens. Låt oss nu utforska de betydande konsekvenserna detta medför.
Trustly Casino Utan Svensk Licens
Trustly, en betalningslösning som har blivit känt för sin enkelhet och snabbhet, är inte längre tillgänglig på casinon utan svensk licens. Detta förbud kan ha en påverkan på din spelupplevelse då Trustly tidigare erbjöd smidig inloggning och snabba uttag.
Notera att Play n Play casinon, som Trustly var en pionjär inom, fortfarande blomstrar. Betalningsmetoder fungerar som en hydra, när en försvinner så poppar två nya upp som fyller samma funktion.
Swish Casino
Swish, känt för sin användarvänlighet och snabba uttag och insättningar när det kommer till casinotransaktioner, är också en av de betalningsmetoder som har blockerats. Detta innebär att du behöver hitta alternativa betalningslösningar om du vill spela på casinon utan svensk licens.
Zimpler Casino Utan Svensk Licens
Zimpler, en populär favorit bland mobilspelare på grund av sin smidiga betalningslösning i mobilen, är numera en annan betalningsmetod som är blockerad. Detta kan innebära en förändring för dig om du föredrar att spela på mobilen och tidigare använde Zimpler för dina transaktioner.
Men oroa dig inte, det finns massor av simpla och smidiga betalningslösningar med minst lika snabba och säkra insättningar och uttag på casino utan svensk licens.
Casino med BankID
Tidigare var BankID en säker och pålitlig inloggnings- och betalningsmetod på casinon utan svensk licens. Nu, med denna metod blockerad, kan vi förvänta oss lanseringen av andra lösningar som InstaBank som fyller precis samma funktion som BankID. Det är en spännande utveckling som ger oss fler alternativ att välja mellan och öka tillgängligheten för spelare.
Casinon Utan Svensk Licens med Snabba Uttag
Nu när vi har analyserat alla olika betalningsmetoder som används på casinon utan svensk licens kommer vi att lista de betalningsmetoder med snabba uttag och även fem casinon utan svensk licens med snabba uttag.
Betalningsmetoder för Snabba Casino Uttag
För att göra snabba uttag på casinon utan svensk licens finns det flera betalningsmetoder att använda. E-plånböcker som Skrill och Neteller är snabba och säkra alternativ med låga avgifter.
Kryptovalutor som Bitcoin kan också erbjuda snabba överföringstider, men med en högre riskprofil. Paysafecard möjliggör snabba överföringar, men endast för insättningar. Se till att noggrant granska casinots uttagspolicy för att undvika förseningar och avgifter. Med dessa kunniga valmöjligheter kan du njuta av smidiga uttag på casinon utan svensk licens.
Fem Casinon Utan Svensk Licens med Snabba Uttag
Låt oss nu dyka in i en djupare översikt över fem utvalda casinon utan svensk licens som utmärker sig med sina snabba uttag. Denna lista ger dig en inblick i de mest tillförlitliga online casinon med snabba, säkra och problemfria insättningar och uttag.
- Mega Dice: Direkta uttag med de flesta metoder (upp till en timme som max)
- SlotAmba: Upp till en timme med kryptovalutor (upp till 32 timmar med banköverföring)
- SupaCasi: Upp till en timme med kryptovalutor, och e-plånböcker (upp till 48 timmar med banköverföring)
- CashAlot: Upp till en timme med kryptovalutor (upp till 48 timmar med banköverföring)
- 21Bets: Upp till en timme med kryptovalutor (upp till 48 timmar med banköverföring)
Pay N Play Casinon Utan Svensk Licens
Pay N Play casinon representerar den moderna generationen av online casinon utan svensk licens, där spelare kan börja spela direkt utan att behöva genomgå en lång registreringsprocess. Dessa casinon utan svensk licens har blivit oerhört populära tack vare sin oslagbara bekvämlighet och blixtsnabba spelupplevelse. De erbjuder en smidig och oavbruten spelupplevelse som gör dem till det självklara valet för spelentusiaster.
När du spelar på ett Pay N Play casino slipper du besvärliga formulär och identitetsverifiering. Med en enkel insättning via din onlinebank kan du snabbt och säkert börja njuta av dina favoritcasinospel. Så upplev den snabba och smidiga processen idag och upptäck fördelarna med Pay N Play!
De flesta Pay N Play casinon utan svensk licens använder Trustly som betalningslösning för att erbjuda denna tjänst. Trustly agerar som en pålitlig mellanhand mellan din bank och casinot, vilket möjliggör smidiga och direkta insättningar samt uttag från ditt bankkonto. Med detta säkerställs att du kan njuta av casinospel utan att oroa dig för att lämna ut känslig information. Pay N Play är därför det självklara valet när det kommer till säkra och pålitliga alternativ för casinon utan svensk licens.
Kom ihåg att även om Trustly och liknande betaltjänster inte är tillgängliga för casinon utan svensk licens, så finns det andra alternativ som erbjuder en liknande smidig och användarvänlig upplevelse. Du kan fortfarande dra nytta av fördelarna med Pay N Play när du spelar på ett casino utan svensk licens.
Casino Utan Konto
Ett casino utan konto, även känt som Pay N Play casino, är ett banbrytande koncept inom online spelvärlden. Det här moderna tillvägagångssättet gör det möjligt för dig att njuta av dina favoritspel nästan direkt, utan krångel med att skapa ett konto. Genom att använda ditt bankID eller ett alternativ till bankID för att verifiera din identitet, sparar du värdefull tid samtidigt som du får en extra nivå av säkerhet.
Ett casino utan konto ger dig snabb och omedelbar tillgång till spel, vilket förbättrar spelupplevelsen och gör det enklare för dig att njuta av spelet utan distraktioner. Du slipper fylla i långa registreringsformulär eller vänta på att ditt konto ska aktiveras. Istället kan du börja spela direkt och få omedelbar tillgång till underhållningen. Upptäck den smidiga och bekväma spelupplevelsen hos ett casino utan konto idag!
Fördelarna med casinon utan konto sträcker sig bortom enkelhet och snabbhet. De erbjuder även en högre nivå av säkerhet genom att inte kräva ytterligare personlig information. Istället verifierar du din identitet direkt via din bank, vilket effektivt minimerar risken för identitetsstöld eller bedrägeri. Dessutom kan du vara trygg i vetskapen att dina transaktioner är skyddade och att dina personuppgifter förblir säkra.
Detta är en banbrytande utveckling inom online casinon utan svensk licens som kommer att förändra spelupplevelsen för många. Om du är trött på att behöva fylla i registreringsformulär och vänta på att ditt konto ska aktiveras, så är ett casino utan konto definitivt något att överväga.
Bästa Casinon Utan Konto 2024
Så, nu när vi har diskuterat fördelarna och funktionaliteten av casinon utan konto, låt oss titta på några av de bästa casinon utan konto som finns tillgängliga 2024 för svenska seplare. Nedan presenterar våra casinoexperter en topplista över fem casinon utan konto som står ut i termer av spelupplevelse, säkerhet, och hastighet.
- Mega Dice: Börja spela direkt utan verifiering
- SlotAmba: Spela inom 30 sekunder från att du besöker hemsidan
- SupaCasi: Sätt in pengar och spela direkt
- CashAlot: Spela utan registrering
- 21Bets: Helt utan verifiering eller registreringsprocess
Nya Casinon Utan Svensk Licens
Spelentusiaster som söker efter unika och innovativa spelupplevelser kommer verkligen att uppskatta den friska fläkt som nya casinon utan svensk licens erbjuder. Dessa casinon har moderna funktioner, lockande bonusar och en unik spelvärld som inte nödvändigtvis finns hos etablerade casinon.
Genom att använda de senaste teknikerna strävar de efter att erbjuda den absolut bästa spelupplevelsen och dra till sig spelare med sin fräscha och spännande approach. Nya casinon strävar efter att verkligen sticka ut från mängden genom att erbjuda något annorlunda och unikt, och det är verkligen värt att utforska vad de har att erbjuda.
Att välja ett nytt casino utan Spelpaus kan också ge dig tillgång till förmånliga bonusar och generösa kampanjer, då de nya aktörerna strävar efter att locka till sig fler spelare. Dessutom ger valet av ett helt nytt casino dig möjlighet att vara en av de första att utforska deras breda spelutbud, vilket kan ge en spännande och underhållande upplevelse.
Emellertid finns det också nackdelar med att välja nya casinon. Även om de kan erbjuda moderna funktioner och attraktiva bonusar, kan de sakna den trovärdighet och erfarenhet som kommer med etablerade varumärken. Dessutom kan de stöta på barnsjukdomar, till exempel tekniska problem eller ofullständigt utvecklad kundtjänst. Det är därför av yttersta vikt att antingen noggrant undersöka det nya casinot innan du gör en insättning eller läsa casinorecensioner.
När det kommer till kritan, står valet mellan ett nytt och ett etablerat casino utan svensk licens helt och hållet på din personliga preferens. Men om du är redo att omfamna spänningen och söker något nytt och unikt, då kan ett nytt casino utan svensk licens vara det ultimata valet för dig. Ta steget och upplev något utöver det vanliga!
Casinolicenser hos Casinon Utan Svensk Licens och Spelpaus
För dig som spelar på casinon utan svensk licens, är det av största vikt att känna till vilken licens som casinot drivs under. Inte bara för att det finns lagliga aspekter att tänka på, utan även för din egen säkerhet och trygghet som spelare. Nedan har vi sammanställt en översikt över de vanligaste casinolicenserna som finns hos casinon utan svensk licens. Dessa licenser är uppdelade i två kategorier: licenser inom EES och licenser utanför EES.
✍ Licenser Inom EES
Inom EES omfattas jurisdiktioner som finns inom Europeiska ekonomiska samarbetsområdet. Dessa licenser tilldelas av välrenommerade och respekterade spelmyndigheter. Låt oss granska några av dem och fördjupa vår kunskap!
✍ Malta Gaming Authority (MGA)
MGA är en av världens mest ansedda licensutfärdare inom EES. Med sina strikta regler och förordningar erbjuder de dig en oöverträffad trygghet när du spelar på ett casino med MGA-licens. Du kan vara helt säker på att du är i professionella händer och kommer att njuta av en exklusiv spelupplevelse i absolut toppklass.
✍ Gibraltar Gambling Commissioner (GGC)
GGC licensierar casinon med stränga standarder för att garantera spelarnas skydd. Vi utför regelbundna kontroller och ser till att casinona följer alla lagar och regler på ett korrekt sätt. Du kan vara trygg i vetskapen att de är dedikerade att upprätthålla högsta nivå av integritet och säkerhet för alla spelare.
✍ Alderney Gambling Control Commission (AGCC)
De har en imponerande historia av att tillhandahålla licenser och har en stark betoning på spelarsäkerhet och rättvisa. Deras engagemang för spelarsäkerhet och rättvisa är välkänt och har sträckt sig över många framgångsrika år.
Licenser Utanför EES
Nu ska vi utforska licenser som utfärdas av licensgivare utanför EES och dess betydelse för dig som spelar på online casinon utan svensk licens.
✍ Curacao eGaming (CGA)
Curacao eGaming är en välkänd licensutfärdare för många casinon på nätet utanför EES. De erbjuder en sömlös licensieringsprocess samtidigt som de strikt upprätthåller regler för att skydda spelarna. Med deras expertis kan du vara trygg och säker när du spelar.
✍ Kahnawake Gaming Commission (KGC)
Baserat i Kanada, är de kända för att utfärda licenser till casinon som erbjuder sina tjänster till spelare över hela världen. KGC strävar efter att förbättra skrivkvaliteten genom att optimera ordval, struktur, läsbarhet och elegans, samtidigt som de behåller den ursprungliga innebörden.
✍ UK Gambling Commission (UKGC)
UKGC är känt för att vara en av de mest strikta licensgivarna när det kommer till att skydda spelare. Casinon som innehar denna licens kan med förtroende garantera en rättvis behandling och fullständig transparens.
Casinospel & Spelutvecklare på Casinon Utan Spelpaus
På online casinon utan spelpaus kan du utforska ett omfattande utbud av spel från världsledande spelutvecklare. Här kan du njuta av allt från tidlösa bordsspel till moderna slots och live casinospel. Få tillgång till spel skapade av välrenommerade utvecklare som NetEnt, Microgaming och Play’n GO, för att bara nämna några.
NetEnt
NetEnt är en av de mest framstående och respekterade spelutvecklarna inom casinobranschen. De erbjuder en omfattande samling av speltyper, inklusive slots, bordsspel och live casinospel.
NetEnt är särskilt kända för sina innovativa slotspel som Starburst och Gonzo’s Quest. Dessa spel är berömda för sin överlägsna kvalitet, imponerande grafik och engagerande spelupplevelse.
Microgaming
Microgaming är en framstående och ledande aktör inom casinobranschen. De är kända för att utveckla några av marknadens mest populära slotspel, såsom Immortal Romance och Thunderstruck II, som erbjuder en oslagbar spelupplevelse.
Utöver slots erbjuder Microgaming också ett imponerande utbud av bordsspel, inklusive blackjack, roulette och baccarat, vilket garanterar en varierad och spännande spelvärld för alla spelentusiaster.
Play’n GO
Play’n GO är en framstående spelutvecklare som stolt erbjuder ett omfattande utbud av högkvalitativa casinospel. Deras expertis sträcker sig från populära slotspel till imponerande bordsspel och videopoker. Bland deras mest älskade spel finner man pärlor som Book of Dead och Fire Joker.
Casinospel hos Casinon Utan Spelpaus
På casinon utan Spelpaus behöver du aldrig kompromissa med kvaliteten. Här erbjuds ett brett utbud av spännande och underhållande casinospel som tilltalar alla smaker. Oavsett om du föredrar klassiska bordsspel, färgsprakande slots eller live casinospel, kan du vara säker på att det finns något för alla. Så låt oss ta ett djupdyk och utforska några av de mest populära spelen!
Slots
Spelautomater är en tidlös klassiker och de mest populära spelen på casinon utan Spelpaus. Dessa spel är enkla att spela, utmärks av fantastisk grafik och ger spelarna en chans att kamma hem stora summor.
Oavsett om du föredrar de klassiska fruktmaskinerna eller moderna videoslots med spännande teman, så kommer du definitivt att hitta något som passar just dig. Våga kasta dig in i spänningen och upptäck de otroliga vinstmöjligheterna som väntar på dig!
Bordsspel
Bordsspel utgör själva hjärtat i varje online casino. Klassiker som Blackjack, Roulette och Baccarat är alltid tillgängliga för spelare som söker en mer strategisk och intellektuell spelupplevelse.
Dessa spel ger dig möjlighet att påverka utfallet genom dina beslut, vilket ökar spänningen ytterligare. Med dessa spel kan du påverka spelet och öka spänningen genom att fatta strategiska beslut som påverkar resultatet.
Live Casino
För en autentisk spelupplevelse rekommenderar vi att du ger live casinospel en chans. Genom att spela med riktiga dealers och livestreams får du verkligen känslan av att vara på ett landbaserat casino, fast du spelar hemifrån.
Dessutom kan du njuta av att chatta med dealern och andra spelare, vilket skapar en social och engagerande spelupplevelse.
Video Poker
Video poker kombinerar det bästa av slots och poker och erbjuder ett snabbt och enkelt spel som kräver skicklighet och strategi för att öka dina vinstchanser. Med flera tillgängliga varianter, inklusive Jacks or Better och Deuces Wild.
På casinon utan Spelpaus kan man utforska olika spel och upptäcka sina favoriter med total frihet. Oavsett om man är en erfaren spelare eller nybörjare, kommer man garanterat att hitta något som passar sin spelstil och budget.
Betting Utan Svensk Licens
Spelbolag utan svensk licens erbjuder spelare ett omfattande utbud av betting utan svensk licens att satsa på, inklusive fotboll, basket, tennis och mycket mer. Dessa spelbolag är licensierade av respekterade utländska myndigheter som UKGC och CGA, vilket garanterar deras pålitlighet och säkerhet.
En av de främsta fördelarna med att spela på bästa bettingsidor utan svensk licens är den fantastiska flexibilitet som spelarna får. Till skillnad från svenska bettingsidor är du inte begränsad av den svenska spelgränsen på 5000 SEK per vecka.
Det innebär att du kan satsa mer pengar om du vill maximera dina vinstmöjligheter. Dessutom slipper du bli avstängd av Spelpaus, vilket är en klar fördel för spelare som har full kontroll över sitt spelande och vill fortsätta njuta av spänningen utan avbrott.
Bästa Casino Utan Svensk Licens och Spelpaus 2024
Mega Dice har etablerat sig som det bästa casino utan svensk licens 2024. Med en imponerande välkomstbonus och relativt låga omsättningskrav har de snabbt blivit en favorit bland spelare. Flexibiliteten hos Mega Dice är oöverträffad, med snabba uttag som gör det enkelt och effektivt för spelarna att njuta av sina vinster.
Förutom detta erbjuder Mega Dice ett omfattande utbud av casinospel och bettingmöjligheter. Oavsett vilken typ av spel du föredrar, kommer du garanterat att hitta något som tilltalar dig. Oavsett om du är en fotbollsentusiast på jakt efter spännande bettingalternativ eller en entusiastisk älskare av spelautomater som söker det senaste inom slots, så har Mega Dice något alldeles extra att erbjuda.
Dessutom är Mega Dice-plattformen otroligt användarvänlig och perfekt anpassad för mobilen. Du kan njuta av spänningen vart du än befinner dig. Mega Dice har fått mycket beröm för sin enastående användarvänlighet, vilket gör det till det bästa valet för alla som söker ett casino utan svensk licens. I en värld där bekvämlighet och tillgänglighet är avgörande, är Mega Dice verkligen det självklara valet.
Avslutande Tankar om Casino Utan Svensk Licens och Spelpaus
Att välja att spela på ett casino utan svensk licens och Spelpaus kan ge spelare fler friheter och möjligheter. Vi har introducerat olika typer av spel som finns tillgängliga på dessa plattformar, inklusive slots, bordsspel, live casinospel och video poker.
Vi har även framhävt fördelarna med att spela på casino utan Spelpaus, såsom högre gränser och ingen avstängning. Vi har utforskat de bästa casinon utan svensk licens 2024, som erbjuder en imponerande användarvänlighet, ett omfattande spelutbud och flexibla bettingmöjligheter. Detta är de viktiga punkterna vi har täckt, och vi hoppas att det ger dig en tydligare bild av fördelarna med att välja casinon och bettingsidor utan svensk licens.
Frågor och Svar om Casino Utan Svensk Licens
Är casinon utan svensk licens licenserade någonstans?
Ja, casinon utan svensk licens är oftast licensierade av andra respekterade myndigheter som UK Gambling Commission (UKGC) eller Malta Gaming Authority (MGA). Dessa licenser garanterar att casinot följer strikta regler och riktlinjer för rättvist spel och säkerhet.
Är ett casino utan svensk licens riggat?
Nej, casinon utan svensk licens använder sig av slumpgeneratorer (RNG) för att säkerställa att alla spelresultat är helt slumpmässiga. Dessutom övervakas de av sina respektive licensutgivare för att säkerställa rättvist spel.
Är det säkert med spel hos casinon utan svensk licens?
Ja, det är säkert att spela på casinon utan svensk licens, så länge de är licensierade av respekterade spelmyndigheter som UKGC, MGA, eller Curaçao eGaming. Dessa licenser garanterar att casinot uppfyller vissa säkerhetsstandarder och skyldigheter.
Är det lagligt att spela hos ett casino utan svensk licens?
Ja, det är lagligt för svenska spelare att spela på casinon utan svensk licens. Däremot kan vissa begränsningar gälla, som att man inte har rätt till samma konsumentbeskydd som med svenska licensierade casinon.
Kan man spela hos casinon utan svensk licens trost Spelpaus?
Ja, Spelpaus gäller endast för casinon med svensk licens. Om du har registrerat dig för Spelpaus men vill fortsätta spela kan du göra det på casinon utan svensk licens.
Erbjuder casinon utan licens insättningsbonusar?
Ja, de flesta casinon utan svensk licens erbjuder attraktiva välkomstbonusar och kampanjer för att locka nya spelare. Bonusvillkoren kan dock variera, så det är viktigt att läsa igenom dessa innan du tar del av en bonus.
Kan man spela på norska casinon utan svensk licens?
Ja, svenska spelare kan spela på norska casinon utan svensk licens. Det är dock viktigt att kolla upp casinots licens och se till att den kommer från en respekterad spelmyndighet.
Hur låg är lägsta insättningen hos casinon utan Spelpaus?
Minsta insättning på casinon utan svensk licens kan variera beroende på casinot och dess betalningsmetoder. Generellt sett kan du förvänta dig att minimibeloppet ligger någonstans mellan 100 och 200 SEK.
Har Spelinspektionen någon auktoritet över casinon utan svensk licens?
Nej, Spelinspektionen har ingen juridisk auktoritet över casinon utan svensk licens.